Pratit Luthra 4 years, 6 months ago sec 2 x=22tanx 1tan 2 x=22tanx tan 2 x2tanx1=0 (tanx1) 2 =0 tanx=1 1 Thank You ANSWER Class12th practical Shivam Mishra, Meritnation Expert added an answer, on 26/7/16 Shivam Mishra answered this Dear Student, Please find below the solution to the asked query We have f 2 tanx 1 tan 2 x = cos 2 x 1 sec 2 x 2 tanx 2 = cos 2 x 1 2 1 cos 2 x 2 sinx cosx = cos 2 x 1 2 1 2 sinx cosx cos 2 x = cos 2 x 1 2 1 sin 2 x cos 2 x = 2 cos 2 x 1 1 2 1 sin 2 x cos 2 x = 2 cos 2 x 2 1 sin 2 x cos 2 x f 2 tanx 1 tan 2 x = 1 sin 2 x We know that 2 tanx 1 tan 2 x = sin 2 x f sin 2Sin2xcos2x = 1 tan2x1 = sec2x sin 2x = 2 sin x cos x cos 2x = 2 cos2x 1 tan x = sin x cos x sec x = 1 cos x cot x = cos x sin x csc x = 1 sin x Some integration formulas R xn dx = xn1 n1 C R 1 x dx = lnjxjC R ex dx = ex C R sin x dx = cos x C R cos x dx = sin xC R
2
F(2tanx/1 tan^2x)=(cos2x 1)(sec^2x 2tanx)/2 then f(1)
F(2tanx/1 tan^2x)=(cos2x 1)(sec^2x 2tanx)/2 then f(1)-In any triangle we have 1 The sine law sin A / a = sin B / b = sin C / c 2 The cosine laws a 2 = b 2 c 2 2 b c cos A b 2 = a 2 c 2 2 a c cos B c 2 = a 2 b 2 2 a b cos C Relations Between Trigonometric FunctionsQuestion Prove The Identity Sec^2/2 Tan X = Csc 2x This problem has been solved!



2
Click here👆to get an answer to your question ️ Match the statements of Column I with values of Column II Column IColumn IIAIf f(x) = x 1 , when x2 tan^2x = 1 tan^2 x x = pi/6 {x is angle expressed in radians} General solution is x = 2* n * pi pi/6 (where n is a natural number) (tan x)× (tan 2x) = 1 or tan x = 1/ (tan 2x) =cot 2x or tan x = tan (pi/2 2x) or x = npi (pi/2–2x) or x2x= (n1/2)pi Misc 1 Misc 2 Important Misc 3 Deleted for CBSE Board 22 Exams Misc 4 Important Deleted for CBSE Board 22 Exams Misc 5 Deleted for CBSE Board 22 Exams Misc 6 Deleted for CBSE Board 22 Exams
Simply tan (AB) = tanAtanB/1tanAtanB From this formula we can derive tan (2x) as tan (xx) So tan (2x)= 2tanx/1tanxtanx We can always go forGet an answer for 'Prove the following sin 2x = (tan x)(1 cos 2x)' and find homework help for other Math questions at eNotes∫ d x cos 2 x = tan x C 2 and by combining the two constants of integration into one, we find the answer (1) ∫ ( 1 tan x) 2 d x = tan x − 2 log cos
Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2 2Solve the equation √3 sin2x cos2x = 0 for π≤x≤π No idea how to approach this one Thanks a if sinx=7/5 and angle x is in quadrant 2 and cos y=12/13 and angle y is in quadrant 1 find sin (xy) asked in TRIGONOMETRY by harvy0496 Apprentice doubleangle



1




Solved Find All Solutions To The Equation Tan 2x 2tanx 1 0 Chegg Com
Rewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x) Explanation 2tanx 1 tan2x = 2 sinx cosx sec2x = 2 sinx cosx 1 cos2x = 2sinx cosx × cos2x 1 = 2sinxcosx Best answer We have f (2tanx/ (1 tan2x)) = 1/2 (1 cos2x) (sec2x tanx) = 1/2x 2cos2x x (1 tan2x 2tanx) = cos2x x (1 tanx)2 = {cosx x (1 tanx)}2 = (cosx sinx)2 = 1 sin (2x) Thus, f (sin 2x) = 1 sin (2x)



What Is The General Solution Of Sec 2 2x 1 Tan 2x Quora




Nwoqnovhk C Gm
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeCos2 (x) (1 tan2 (x)) = 1 cos 2 ( x) ( 1 tan 2 ( x)) = 1 Replace the cos2(x) cos 2 ( x) with 1−sin2 (x) 1 sin 2 ( x) based on the sin2(x)cos2(x) = 1 sin 2 ( x) cos 2 ( x) = 1 identity 1−sin2 (x)(1tan2(x)) = 1 1 sin 2 ( x) ( 1 tan 2 ( x)) = 1 Simplify each term Tap for more stepsSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Tan2x 1 ただの悪魔の画像




Tanx 4 3 X In Quadrant Ii Find The Value Of Sinx 2 Cosx 2 Tanx 2
You can put this solution on YOUR website! Solve the equation 2cos2x = √3 for 0°≤x≤360° I did this cos2x = √3 /2 2x=30 x=15 x=15, 165, 195, 345 Is this correct?Answer (1 of 4) In Trigonemetry Laws and Identities, there are some rule that we will use to prove 1 / sec² (x) = cos² (x) * tan² (x) 1 = sec² (x) * sin² (x) cos² (x) = 1 * tan (x) = sin (x) / cos (x) We will prove from the Left Hand Side We know that sec² (x) = tan² (x) 1, so 1 /




How Do You Solve Sec 2x 2tanx 0 Socratic



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
Trigonometry Solve for x tan (2x)= (2tan (x))/ (1tan (x)^2) tan(2x) = 2tan(x) 1−tan2 (x) tan ( 2 x) = 2 tan ( x) 1 tan 2 ( x) Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan ( x) 1 tan 2 ( x) = tan ( 2 x)Sin(2x) = (2tan(x)) / (1tan^2(x)) *** Start with RHS 2tanx/(1tan^2x) 2tanx/(sec^2x) 2(sinx/cosx)/(1The equation `sec^2x 2*tan x = 4` has to be solved for x Using the basic identity `sin^2x cos^2x = 1` , it is possible to express sec x in terms of tan x




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




5 If F 2tan X 1 Tan 2 X Qquad Cos2x 1 Sec 2 X 2tan X
If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X bestpictjcry Tan 2x Tan 2x Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo Example 14 Show Tan 3x Tan 2x Tan X Tan 3x Tan 2x Tan X Find The Range Of F X Sqrt 4 Sqrt 1 Tan 2x 3 Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2xWhy create a profile on Shaalaacom? Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 ta



Tan2x 1 ただの悪魔の画像



bestpictjcry Tan 2x Tan 2x
`f((2tanx)/(1tan^2x))=((cos2x1)(sec^2x2tanx))/2` Step by step solution by experts to help you in doubt clearance & scoring excellent marks in examsAnswer (1 of 7) Here, tan x = 1/2 We know that, the relation between tan x and sec x is sec^2xtan^2x=1 Using this relation, first, we will determine the value of cos x and then, we will determine the value of sin x So now, sec^2xtan^2x=1 => sec^2x(1/4)=1 => sec^2x=1(1/4) => sec^2x=Weekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Annual Subscription $3499 USD per year until cancelled




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55
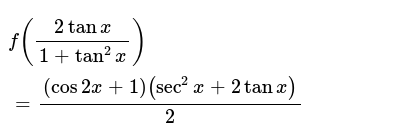



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
If tan x = 2, then y / x = 2 / 1 Then, using, √(x 2 y 2) = r √(2 2 1 2) = √5 = r So sin x = y/r = 2/√5 And using cos 2x = 1 2(sin x) 2 cos 2x = 1 2(2/√5) 2 cos 2x = 1 2 (4/5)Sec(x)^22=tan(x)^2 Replace the with based on the identity Subtract from Move all terms containing to the left side of the equation Tap for more steps Subtract from both sides of the equation Simplify the left side of the equation Tap for more steps Rewrite as Factor out ofThe first derivative of the trigonometric function of tangent with respect to its argument is the reciprocal of the trigonometric function of cosine squared Snarf!




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




If F 2tanx 1 Tan2x Then F 4 Youtube
2tanx/(1tan^2x) sin^2x= =(1cos(2x))/2 (1cos(2x))/2 0 I have two problems I am stuck on, if you could show me how to solve the problems it would be much appreciated 1) Find sin 2x, cos 2x, and tan 2x from the given information tan x = − 1/6, cos x > 0 sin 2x = cos 2x = tan 2x = Math Prove the identity sec^4x tan^4x = 12tan^2x calculus Let F(x)= the integral from 0 to 2x of tan(t^2) dt Use your calculator to find F″(1) By applying the fundamental theorem of calculus, I got the derivative of the integral (F'(x)) to be 2tan(2x^2) When I




Find The Range Of Functionfx 1 2tan 11 X2 P 4




Derivatives Of Tan X And Cot X Video Khan Academy
I just want to ask The equation says tan2x=2tanx/1tan^2x How did it become 2tanx and 1tan^2x?I need to use the fact that $\tan 2x=\sin2x \ /\cos2x$ to prove that $$\tan 2x=\frac{2\tan x}{1\tan^2x}$$ I don't know where to start Please help or hint Thanks in advance sec=4 find sin(2x), cos(2x), tan(2x) These problems seem straight forward but I keep getting the wrong answer If you could please in detail show me how to solve this I would really, really, really appreciate it so I don't throw my Trig book out the window
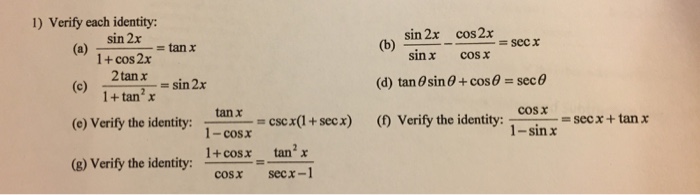



Solved Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com




Tan2x ただの悪魔の画像
Evaluate $\displaystyle \large \lim_{x \,\to\, \tan^{1}{3}} \normalsize {\dfrac{\tan^2{x}2\tan{x}3}{\tan^2{x}4\tan{x}3}}$ Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes1 Your solution is not very rigorous after 0 = t a n 2 x 2 t a n x − 1 After that line, the equation should be t a n x = − 2 ± 2 2 − 4 ( 1) ( − 1) 2 ( 1) Also, after that, it's t a n x = 2 − 1 ≈ or t a n x = 2 1 ≈ Then, x = t a n − 1 ( ) ≈ 225, 25 Share edited May 7 '14 at 1125 answered May



2




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
Trigonometry 1Solve tan^2x tan x – 1 = 0 for the principal value (s) to two decimal places 6Prove that tan y cos^2 y sin^2y/sin y = cos y sin u0004y 10Prove that 1tanθ/1tanθ = sec^2θ2tanθ/1tan^2θ 17Prove that sin^2wcos^2w/tan w sin w cos w tan w = The limit of multiplication of the functions can be split as product of their limits as per the product rule of limits = ( lim x → 0 2 1 − tan 2 x) × ( lim x → 0 x tan 3 x ( 1 − cos 2 x) 2) Now, find the limit of the first factor by the direct substitution but do1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information
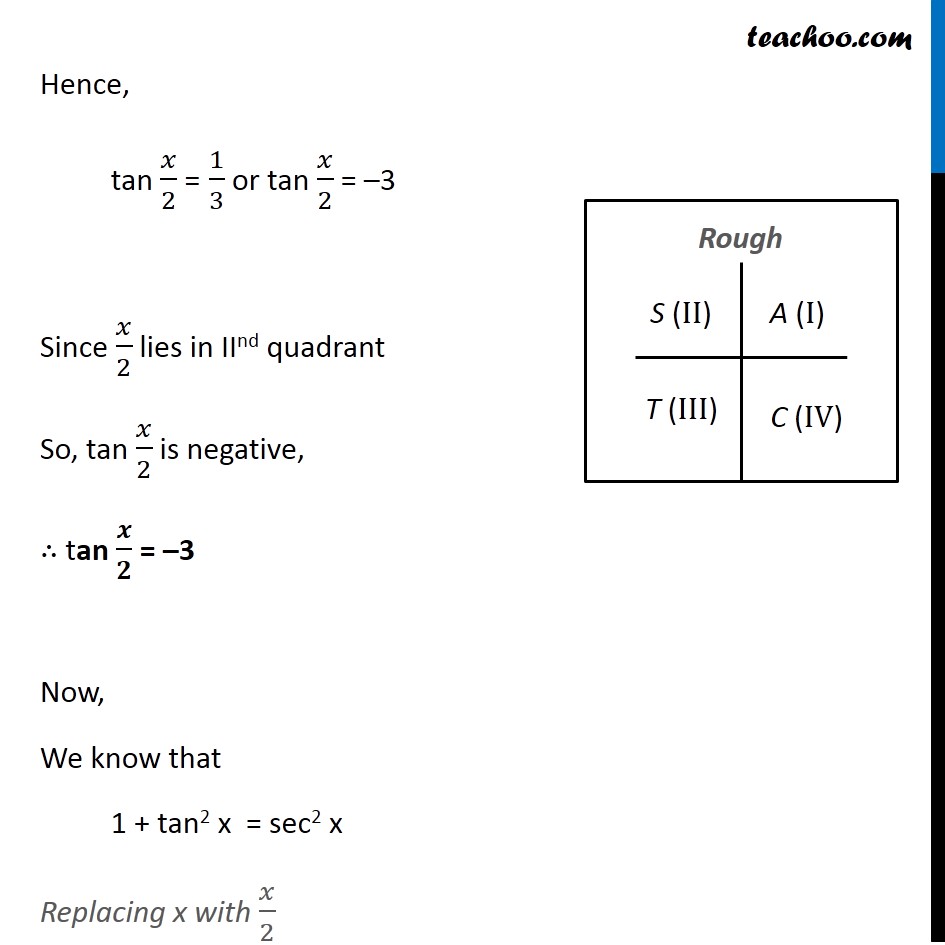



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
See the answer Show transcribed image text Expert Answer 100% (3 ratings) Previous question Next question Transcribed Image Text from this Question Prove the identity sec^2/2 tan x = csc 2xI am unable to see why $$1 \tan^2 x= 1/\cos^2x$$ I have looked into the topic anad I am familiar with the reciprocal ratios of cosec, sec, and cot but cannot derive how this statement makes sense Any help on the topic would be very much appreciated Use trig identities 1 tan^2 x = 1/cos^2 x = sec^2 x (1 tan x) = 1 tan^2 x 2tan x = sec^2 x 2tan x




If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X
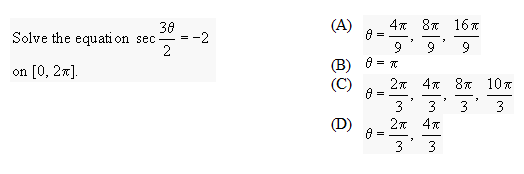



Solved Find All Solutions To The Equation Tan 2x 2tanx 1 0 Chegg Com
(1tan^2x)/(1tan^2(x)) 1 = 2cos^2(x) The trigonometric equation is sec 2 (x) tan x = 2tan(x) tan x sec 2 (x) 2 = 0 ⇒tan x = 0 and sec 2 (x) 2 = 0 tan x = 0 tan x = tan 0 The genaral solution of tan(θ) = tan(α) is θ = nπ α, where n is an integer ⇒ x = nπ 0 x = nπn = 0,1,2 sec 2 (x) 2 = 0 sec 2 (x) = 2 Using reciprocal identity sec 2 x = 1/cosProve as an identity;



Relating Trigonometric Functions Trigonometry Socratic




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
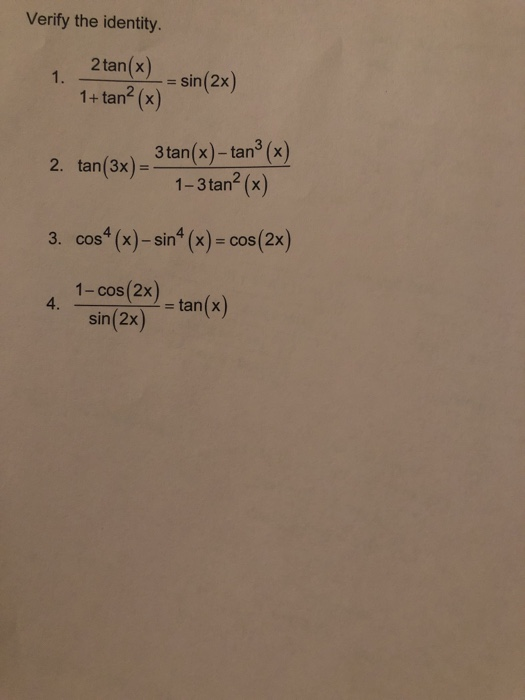



Solved Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube



3




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2



How To Show That Sec X Tan X 1 Sec X Tan X Quora



Is Tanx 2 2tanx 1 5tanx Sec X Quora




Cos 2x



Bestpixtajpgjgh If F 2tanx 1 Tan 2x 1 Cos2x Sec 2x 2tanx 2 Then F 4




Cosec 1 1 Tan 2x 2tanx Youtube




いろいろ Tan2x 1sec2x ただの悪魔の画像




Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3 Check All That Apply Options Are In Brainly Com



How To Find Least Value Of Cos 2 X Sec 2 X Quora




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube



How To Find Least Value Of Cos 2 X Sec 2 X Quora
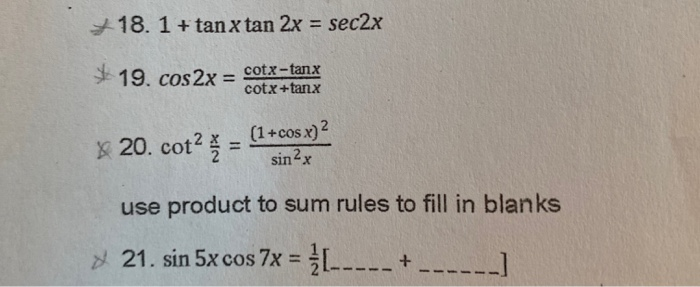



Solved 18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com




If Sec Tita X 1 4x Sec Tita Tan Tita 2x Or 1 2x Mathematics Topperlearning Com 15o2fj
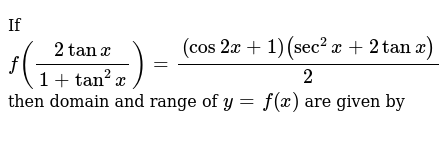



いろいろ Tan2x 1sec2x ただの悪魔の画像




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
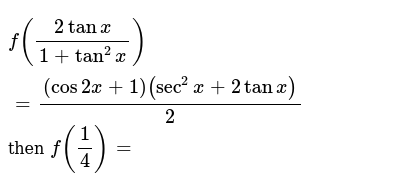



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then F 1




Tan 2x Formula What Is Tan 2x Formula Examples




Prove That 1 Sin 2x Cos 2x 1 Sin 2x Cos 2x Tan X Youtube
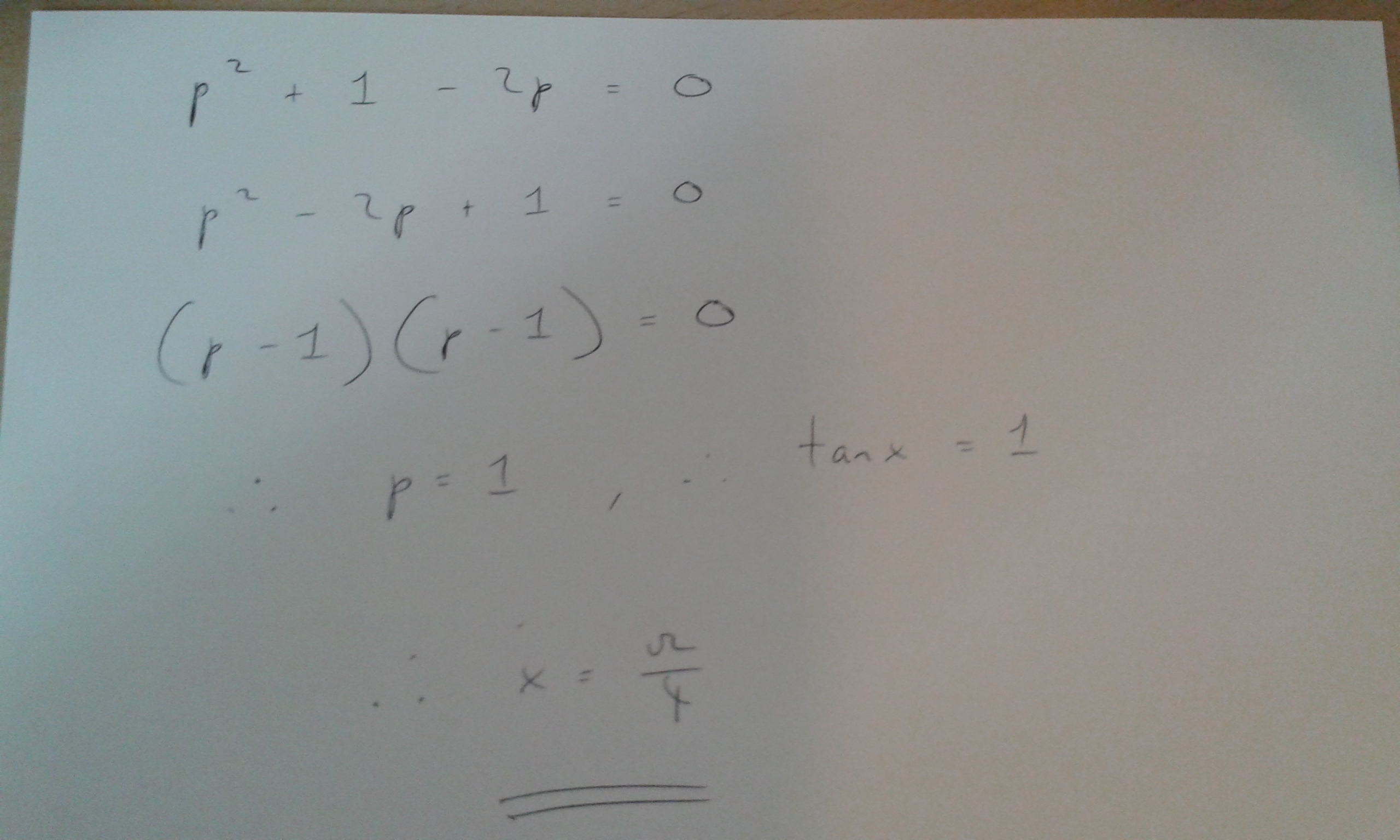



How Do You Solve Sec 2x 2tanx 0 Socratic




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Solved Question 1 Integrate The Following Function Sec 2x Chegg Com




If F X Tan 2x Then



Domaine De Definition De Tan 2x




Tan2x ただの悪魔の画像



How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora



What Is The Integration Of Tan 2x Solution Quora



bestpictjcry Tan 2x Tan 2x




いろいろ Tan2x 1sec2x ただの悪魔の画像




Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Derivatives Of Tan X And Cot X Video Khan Academy



How To Evaluate Tan 2 Tan 1 1 5 Pi By 4 Quora




Old Version Trig Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube




Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2




Trigonometry Solutions Manual



Prove The Identity Tan P 4 X Tan P 4 X 2 Sec 2x Sarthaks Econnect Largest Online Education Community



1



2




Tan2x ただの悪魔の画像



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



2




Proof For Tan 2x 2tanx 1 Tan X Trigonometry Youtube




If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube




Trigonometric Identities Pdf



Tan2x ただの悪魔の画像




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



Evaluate Lim X P 4 Sec 2x 2tanx 1 Cos4x Sarthaks Econnect Largest Online Education Community




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Prove Sin2x 2tanx 1 Tan 2x Socratic



Tan2x ただの悪魔の画像




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Solved 2tan X 2 Sec X 27 Tan 2x 14 Use A Sum Or Chegg Com




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



Is Tanx 2 2tanx 1 5tanx Sec X Quora
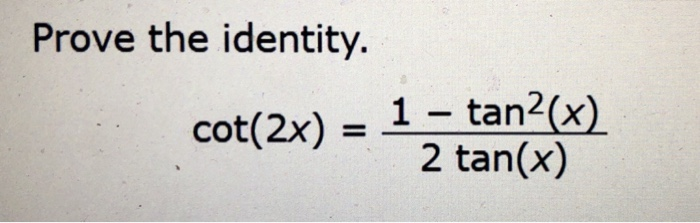



Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com




いろいろ Tan2x 1sec2x ただの悪魔の画像




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Powers Of Trigonometric Functions




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Limit X 0 Xtan2x 2xtanx 1 Cos2x 2 Equals
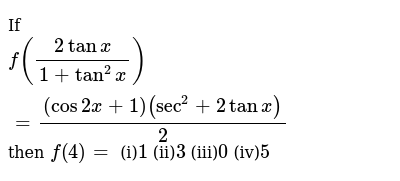



If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2




Find All Solutions In 0 2pi A 2tan 2x 3 B Cos 2x Sin 2x 1 Homeworklib




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Pw7jvk9kgjfojm




Exponential Functions Frac D D X Left X E X Right Y Y X E 2




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2



2
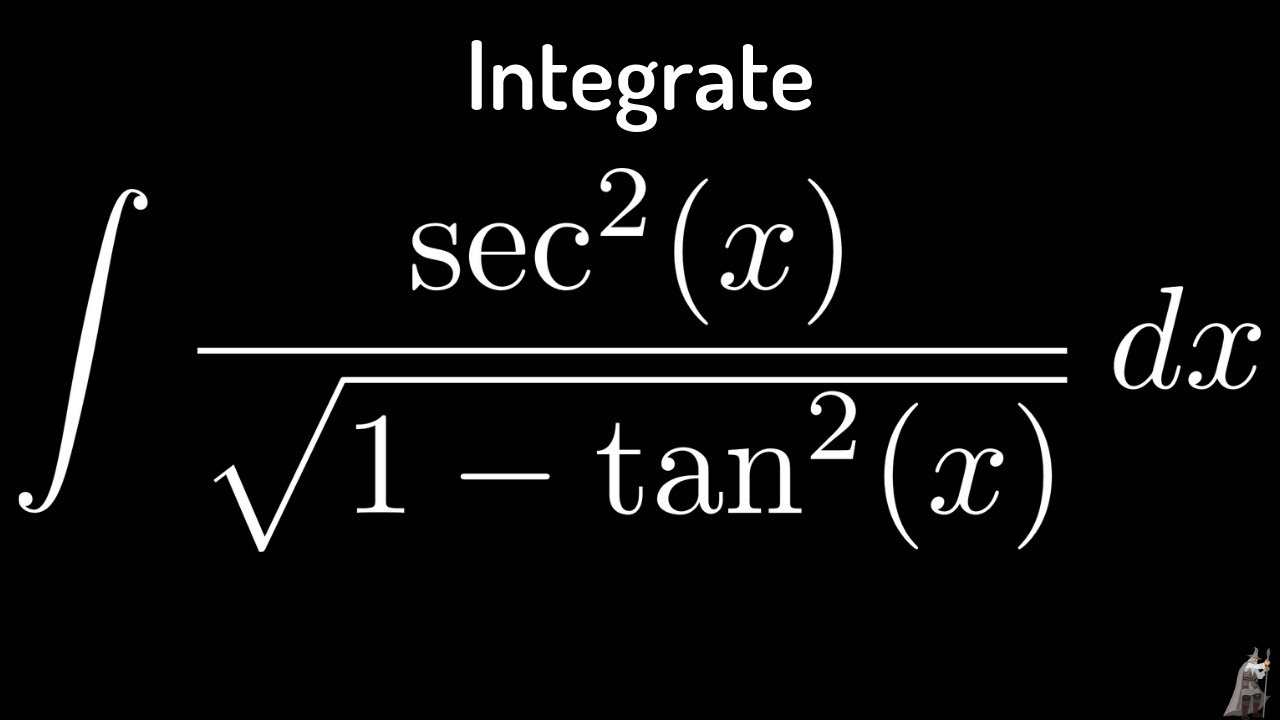



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube



1



Trig Identities Crossword Wordmint



A 1 Tan X Tan X 1 Show That A Ta 1 Cos 2x Sin 2x Sin 2x Cos 2x Sarthaks Econnect Largest Online Education Community



0 件のコメント:
コメントを投稿